Optimum Blade Loading Secondary Flow Reduction in Subsonic Impellers

Across the specific speed range, compressors are subject to various flow phenomena and loss mechanisms which are dominant in that particular range. For example, leakage and secondary flow effects are more dominant in lower ranges, whereas profile/shock losses and corner separation in diffusers take priority in the higher ranges. In this article, we focus on secondary flow effects and how to come up with a set of optimal design guidelines to suppress this particular loss mechanism in a compressor.

The case being discussed here, shown in Figure 1, is a typical industrial compressor stage which is used as part of a multi-stage centrifugal compressor environment. The stage consists of an impeller and a vaneless diffuser coupled with a return channel, but the focus will remain on the isolated impeller in this discussion.

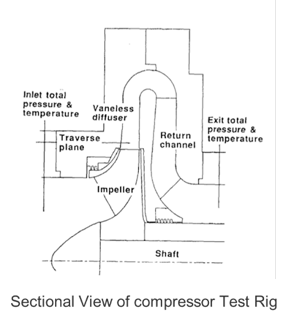
Figure 1: Sectional view of the compressor stage and test rig

Secondary Flows in Impellers

Generally, the dominant source of loss in subsonic impellers is secondary flows. Thus, the specified loading type should be aimed at controlling these secondary flows. Figure 2 shows the actual flow field that was predicted for the conventional impeller:

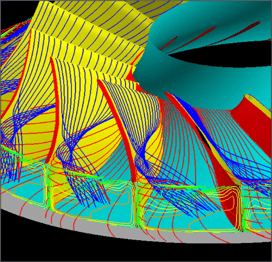
Figure 2: Secondary flows in a conventional subsonic impeller

The streamlines, that were created very close to the blade suction surface, reveal strong secondary flows moving the low momentum fluid that is generated on the suction surface from the hub towards the shroud trailing edge region. It can also be seen that these low momentum fluids in the boundary layer are being moved by the secondary flows and result in the formation of exit flow non-uniformity at the exit of the impeller, which can result in:

• high mixing losses
• high diffuser and stage losses
• compressor instability at least in the case of vaned diffusers

As this is one of the major sources of loss for many industrial applications at least for subsonic impellers, the optimum blade loading should be aimed at reducing this exit flow non-uniformity.

Secondary Flow Theory

From Classical Secondary Flow theory (Zangeneh et al, 1988) it can be shown that:

Here W is the velocity, Ω is the absolute vorticity, and so (W.Ω) is the streamwise vorticity. Therefore, this shows that streamwise vorticity will be generated along a streamline if there is a component of vorticity in the direction of streamline curvature acceleration or a component of vorticity in the direction of Coriolis acceleration. Based on this, the rotating channel can be divided into these three parts:

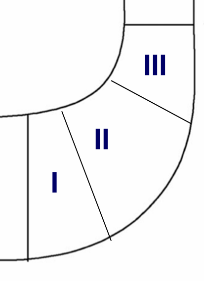
Figure 3: Rotating channel sections

Generally, there are negligible secondary flows in the inducer region since the boundary layer has not grown very much. Also, the radial section mainly sees the tangential component of Coriolis acceleration. However, when it comes to section 2 (axial to radial bend), there are multiple contributions resulting in secondary flows on the hub from the pressure surface to the suction surface. These then finally get moved up along the suction surface and are then dumped near the trailing edge. So, what the above equation shows is that in section 2, there are very complex secondary flow patterns moving low momentum fluids both at the endwalls and the blade surfaces, and then moving all these losses to the tip trailing edge plane.

In fact, the momentum equation can be used to express the Coriolis and streamline curvature accelerations in terms of gradients of reduced static pressure as follows:

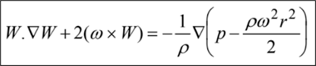
This is for incompressible flow, whereas for compressible flow this will be enthalpy. It can be shown then that secondary flows are generated whenever there is a gradient of reduced static pressure (or relative Mach number in the case of compressible flows) in the direction of vorticity in the flow field. Eventually, this becomes a very easy way of looking at the problem and solving the issue.

Blade Surface Mach Number

If the relative Mach number on the conventional impeller blade is plotted as in Figure 4, it can be observed that the secondary flows are driven by the difference between the suction surface of the shroud and the suction surface of the hub. Therefore, if this gap can be reduced, then it should be possible to suppress the secondary flows. In the inverse design method, it is possible to directly control the pressure jump across the blade or the blade loading and therefore, by making appropriate changes to the blade loading, we could very easily adjust the overall surface Mach number in such a way that we reduce the gap, as we show in this example. And this should then help to reduce secondary flows in the impeller.

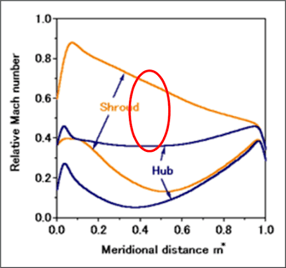
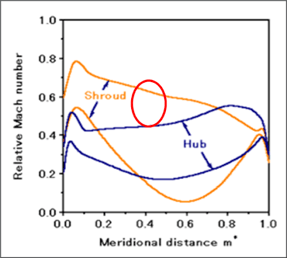
Figure 4: Surface Mach number distribution on conventional (left) and inverse (right) impeller

Optimum Loading for Secondary Flow Control

The type of loading that can be used for this purpose is a fore-loaded distribution at the shroud and an aft-loaded distribution at the hub (Figure 5). The net effect of this type of change is that essentially, it helps raise the suction surface hub velocity and reduce the suction surface shroud velocity, and therefore reduces the gap mentioned earlier. This is essentially what we are trying to achieve here, and is the key element of the approach. It may be noted here that this approach works in the case of pumps as well.

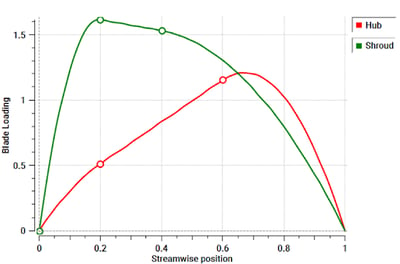
Figure 5: Optimum blade loading for secondary flow control in compressors

CFD Results for TURBOdesign1 Impeller

The compressor shown earlier was redesigned, and the reduction of the secondary flows on the suction surface is clearly visible in Figure 6. In the redesign, very little secondary flows remain on the suction surface, resulting in a much more uniform exit flow. Also shown alongside are experimental results from the same test facility consisting of the impeller, the vaneless diffuser and the return channel. These stage results use the total pressure and total temperature at the inlet of the impeller and the exit of the return channel, and using that data, a 5-point improvement in efficiency could be achieved. Therefore, the key takeaway is that a more uniform exit flow not only benefits the impeller, but also the stage as a whole through reduction in mixing losses.

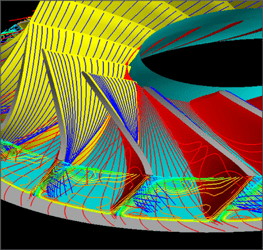
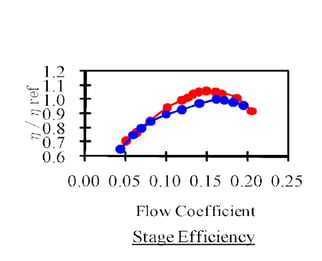
Figure 6: Secondary flow suppression in inverse designed impeller (left) and comparison of measured stage results (right)

Comparison of Blade Angle

Figure 7 presents the blade angle differences between the conventional and the inverse impeller. Many conventionally designed impellers have very similar blades to this, whereas the resulting inverse design blade angles are clearly very different. This is probably one of the reasons why, perhaps even though the nature of secondary flows was well understood for many years, it was very difficult with conventional approaches to try and suppress secondary flows in a systematic way in the impeller.

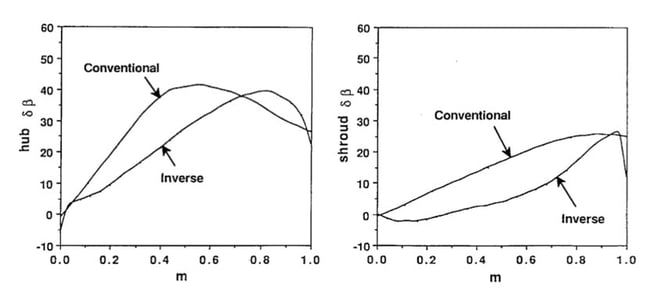
Figure 7: Blade angle comparison between conventional and inverse-designed impellers